深入理解注意力机制【Self-Attention,自注意力模型】
在自然语言处理领域,注意力机制(Attention Mechanism)已经成为提升模型性能的重要工具。传统的Encoder-Decoder结构在处理长序列时,常常因为统一语义特征向量的长度限制而导致性能瓶颈。然而,注意力机制通过引入动态上下文向量,成功解决了这一问题,使得模型能够在每个时间步选择与当前输出最相关的信息。
本篇博客将详细介绍注意力机制的基本原理、一般形式以及自注意力模型,并通过具体例子和图示来更好地理解这些关键概念。
一、语言模型实例
在Encoder-Decoder结构中,Encoder把所有的输入序列都编码成一个统一的语义特征c再解码:
因此, c中必须包含原始序列中的所有信息,它的长度就成了限制模型性能的瓶颈。如机器翻译问题,当要翻译的句子较长时,一个c可能存不下那么多信息,就会造成翻译精度的下降。
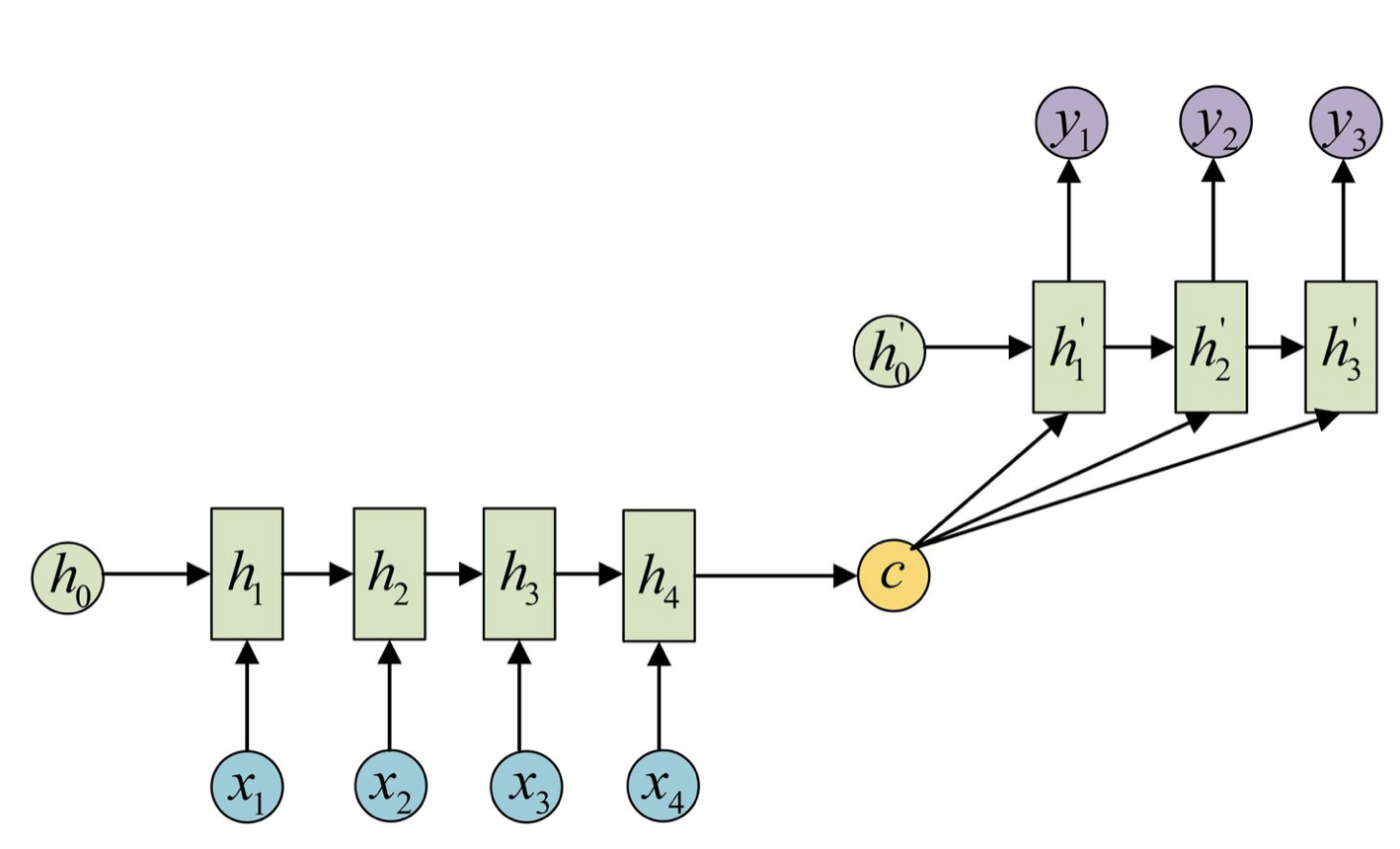
Attention机制通过在每个时间输入不同的c来解决这个问题,下图是带有Attention机制的Decoder:
每一个c会自动去选取与当前所要输出的y最合适的上下文信息。具体来说:
- 用 $a_{i j}$ 衡量 Encoder中第j阶段的$h_j$和解码时第i阶段的相关性;
- 最终Decoder中第i阶段的输入的上下文信息 $c_{i}$ 就来自于所有 $h_{j}$ 对 $a_{i j}$ 的加权和。
以机器翻译为例(将中文翻译成英文):
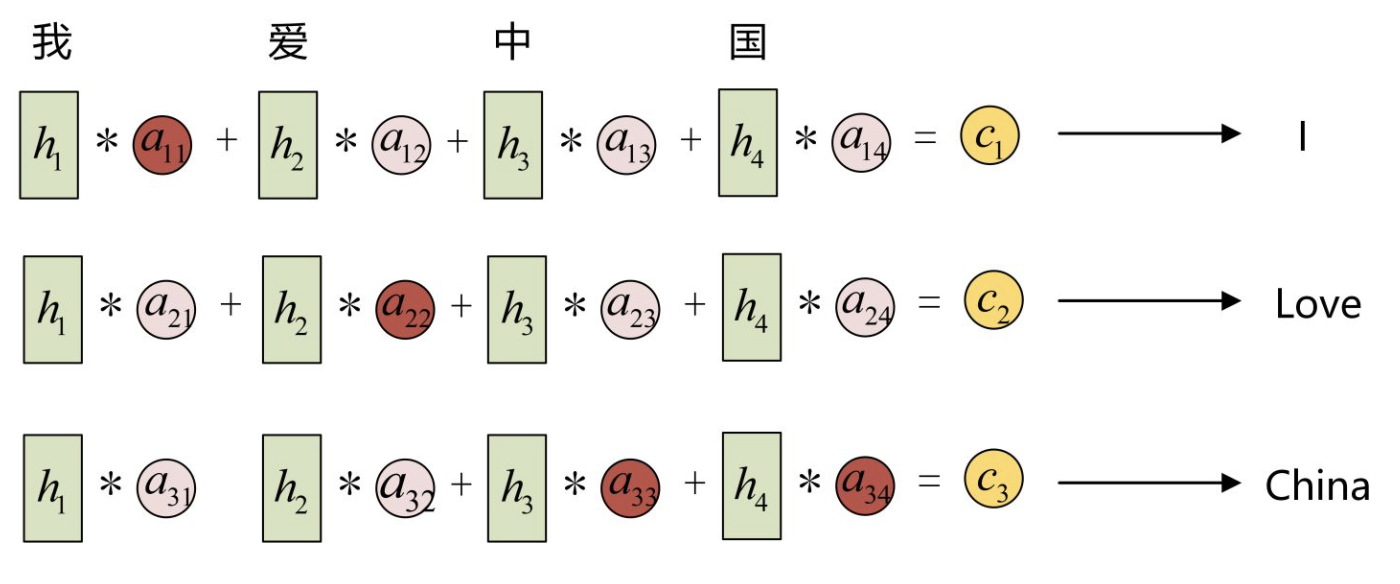
输入的序列是“我爱中国”:
- 因此, Encoder中的h1、h2、h3、h4就可以分别看做是“我”、 “爱”、“中”、“国”所代表的信息;
- 在翻译成英语时, 第一个上下文$c_1$应该和“我”这个字最相关, 因此对应的 $a_{11}$ 就比较大, 而相应的 $a_{12} 、 a_{13} 、 a_{14}$ 就比较小;
- c2应该和“爱”最相关, 因此对应的 $a_{22}$ 就比较大;
- 最后的$c_3$和$h_3、h_4$最相关, 因此 $a_{33} 、 a_{34}$ 的值就比较大。
这些权重 $a_{i j}$ 是怎么来的?事实上, $a_{i j}$ 同样是从模型中学出的, 它实际和Decoder的第i阶段的隐状态、Encoder第j个阶段的隐状态有关,在下面一小节我们会介绍$a_{ij}$如何计算.
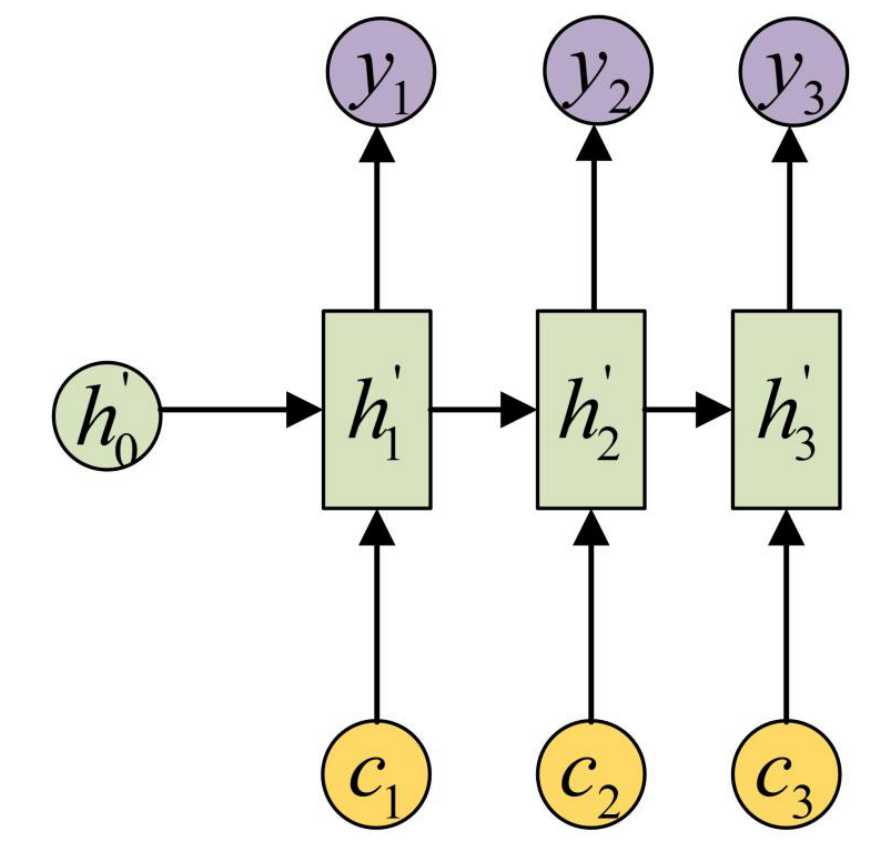
- 这里的$c_1,c_2,c_3$就是attention值;
二、一般模型
刚刚我们是基于Encoder-Decoder模型来介绍attention机制的,下面我们更一般的来介绍注意力机制.
用$X=[x_1,\cdots,x_N]\in\mathbb{R}^{D\times N}$ 表示$N$组输入信息,其中$D$ 维向量 $\boldsymbol{x}_n\in$ $\mathbb{R}^D,n\in[1,N]$表示一组输入信息.为了节省计算资源,不需要将所有信息都输入神经网络,只需要从$\boldsymbol X$ 中选择一些和任务相关的信息.注意力机制的计算可以分为两步:
- 一是在所有输入信息上计算注意力分布;
- 二是根据注意力分布来计算输入信息的加权平均.
为了从$N$个输入向量$[\boldsymbol x_1,\cdotp\cdotp\cdotp,\boldsymbol x_N]$中选择出和某个特定任务相关的信息,我们需要引入一个和任务相关的表示,称为查询向量(Query Vector), 并通过一个打分函数来衡量每个输入向量和查询向量之间的相关性. 给定一个和任务相关的查询向量$\boldsymbol q$,我们用注意力变量$z\in[1,N]$来表示被选择信息的索引位置,即$z=n$ 表示选择了第$n$ 个输入向量.为了方便计算,我们采用一种“软性”的信息选择机制.首先计算在给定$q$和$X$下,选择第$n$个输入向量的概率$\alpha_n$,
\[\begin{aligned}\alpha_{n}&=p(z=n|X,\boldsymbol{q})\\&=\operatorname{softmax}\left(s(\boldsymbol{x}_n,\boldsymbol{q})\right)\\&=\frac{\exp\left(s(\boldsymbol{x}_n,\boldsymbol{q})\right)}{\sum_{j=1}^N\exp\left(s(\boldsymbol{x}_j,\boldsymbol{q})\right)},\end{aligned}\]其中$\alpha_n$ 称为注意力分布( Attention Distribution),$s(\boldsymbol x,\boldsymbol{q})$ 为注意力打分函数.
注意力打分函数$\mathbf{s}(\mathbf{x},\mathbf{q})$:计算输入向量和查询向量之间的相关性,常用如下模型
\[\begin{aligned}&\bullet\text{ 加性模型: }\mathbf{s}(\mathbf{x},\mathbf{q})=\mathbf{v}^{T}\mathrm{tanh}(\mathbf{W}\mathbf{x}+\mathbf{U}\mathbf{q}).\\&\bullet\text{ 点积模型: }\mathbf{s}(\mathbf{x},\mathbf{q})=\mathbf{x}^{T}\mathbf{q}.\\&\bullet\text{ 缩放点积模型: }\mathbf{s}(\mathbf{x},\mathbf{q})=\frac{\mathbf{x}^{T}\mathbf{q}}{\sqrt{D}}.\\&\bullet\text{ 双线性模型: }\mathbf{s}(\mathbf{x},\mathbf{q})=\mathbf{x}^{T}\mathbf{W}\mathbf{q}.\end{aligned}\]这里$\mathbf{W},\mathbf{U},\mathbf{v}$为可学习的参数,$D$为输入向量的维度.
Note:
- 在前面的例子中,$h_1,h_2,h_3,h_4$就是输入向量$X$;
- $h’_1,h’_2,h’_3$就是查询向量$q$;
- $a_{ij}$就是注意力分布,这里我们给出了注意力分布怎么计算的.
得到注意力分布后,对输入向量加权平均可以得到attention值:
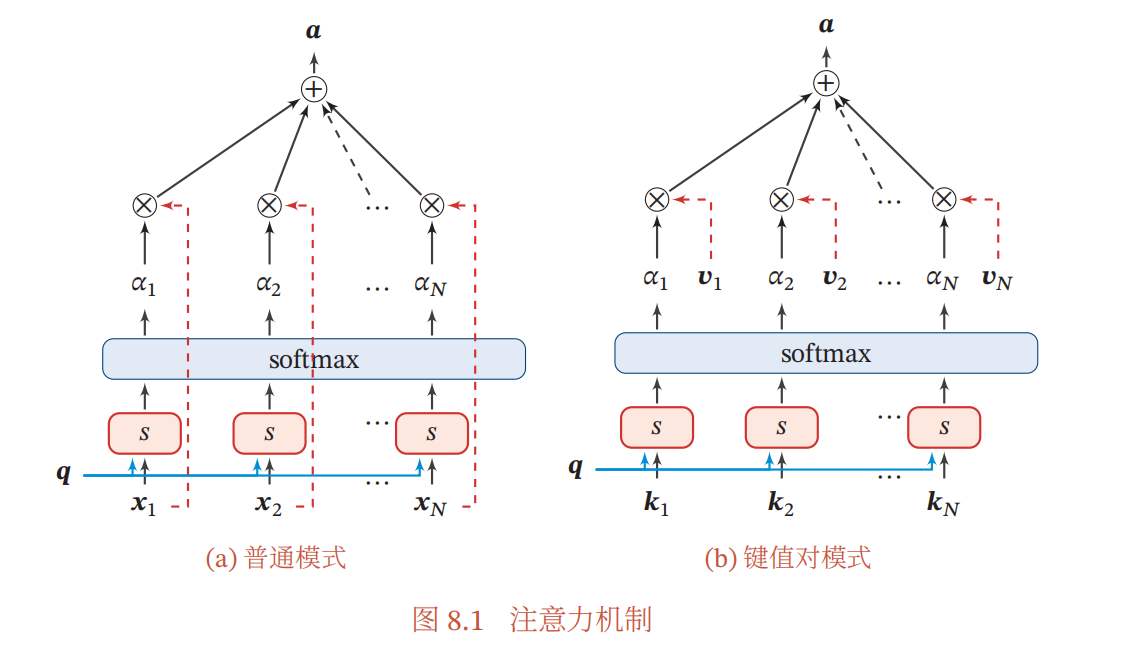
\[\begin{aligned}\operatorname{att}(X,\boldsymbol{q})&=\sum_{n=1}^N\alpha_nx_n,\\&=\mathbb{E}_{z\sim p(z|X,\boldsymbol{q})}[x_z].\end{aligned}\]下图(a)清晰的描述了attention的计算过程.
更一般地,我们可以用键值对( key-value pair)格式来表示输入信息,其中“键”用来计算注意力分布$\alpha_n$,“值”用来计算聚合信息.用$\left(\boldsymbol{K},\boldsymbol{V}\right)=\left[\left(\boldsymbol{k}_1,\boldsymbol{\upsilon}_1\right),\cdots,\left(\boldsymbol{k}_N,\boldsymbol{\upsilon}_N\right)\right]$表示$N$组输入信息,给定任务相关的查询向量$q$时,注意力函数为
\[\begin{aligned}\operatorname{att}\Big((\boldsymbol{K},\boldsymbol{V}),\boldsymbol{q}\Big)&=\sum_{n=1}^N\alpha_n\boldsymbol{v}_n,\\&=\sum_{n=1}^N\frac{\exp\left(s(\boldsymbol{k}_n,\boldsymbol{q})\right)}{\sum_j\exp\left(s(\boldsymbol{k}_j,\boldsymbol{q})\right)}\boldsymbol{v}_n,\end{aligned}\]其中 $s(\boldsymbol{k}_n,\boldsymbol{q})$ 为打分函数.图8.1给出键值对注意力机制的示例.当$K=V$时,键值对模式就等价于普通的注意力机制.
三、自注意力模型(Self-Attention)
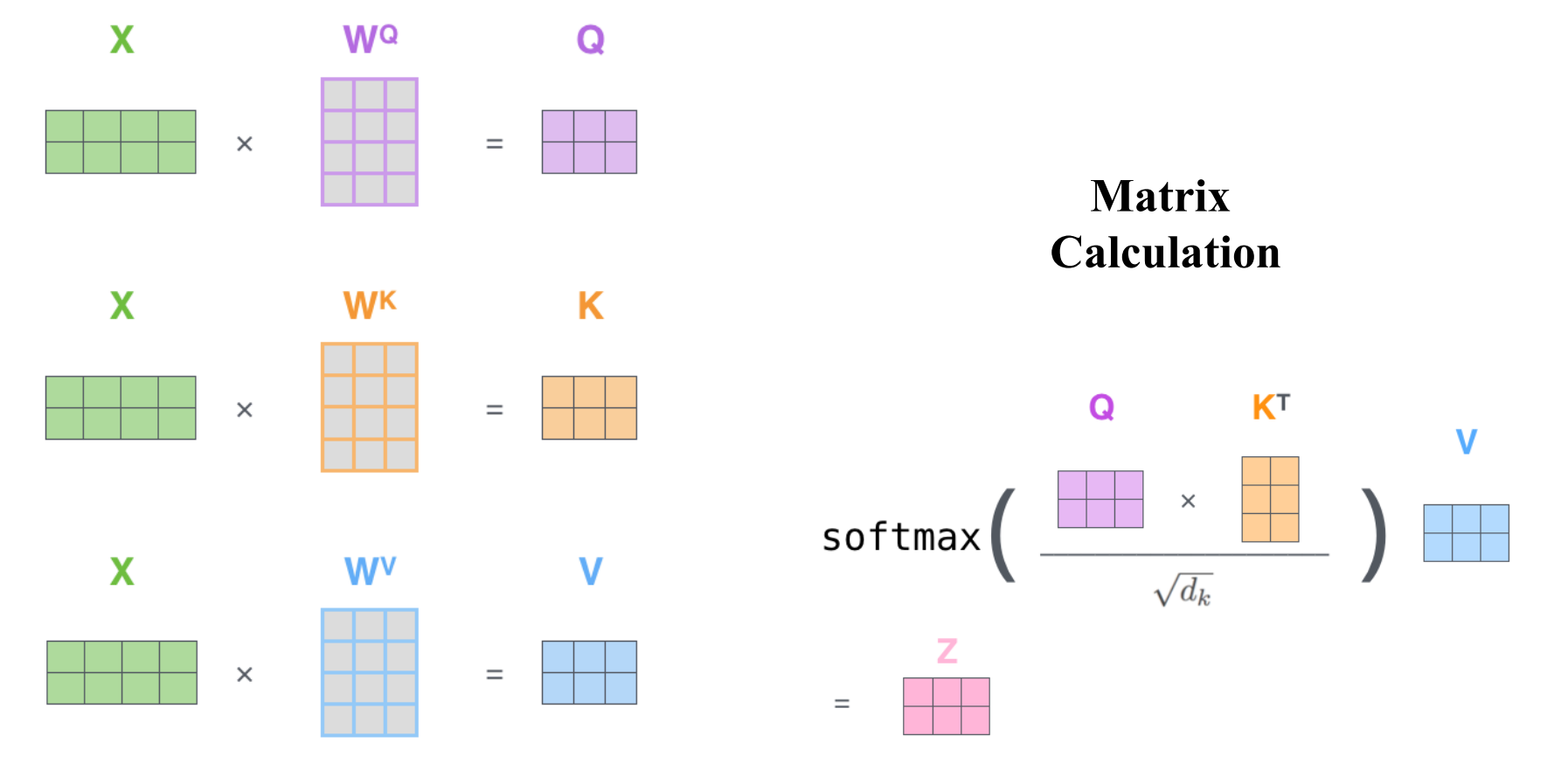
由键值对注意力模式我们可以进一步引出 自注意力模型的概念,该模型通过注意力机制可以建立输入序列长距离依赖关系。自注意力模型计算过程如下图所示:
🔥Note:
- $X$为输入矩阵;
- $W^Q、W^K、W^V$是可学习的参数矩阵;
- 最后得到的$Z$为attention值矩阵;
为什么叫自注意力模型呢?因为我们可以看到这里Q、K、V都是由$X$通过一个线性变换投影得到的,而矩阵$W$是可学习的,所以由$X$到$Z$的映射权重是可学习的,是动态调整的。
如下图所示,红色表示当前的词,蓝色阴影表示与红色词的相关程度,通过自注意力模型,我们可以自动学到每个词与前面词的相关关系。
四、Self-Attention模型的复杂度分析
总的来说,自注意力模型的时间和空间复杂度与输入序列长度$N$呈2次关系,可以不严格的表示为$O(N^2)$.
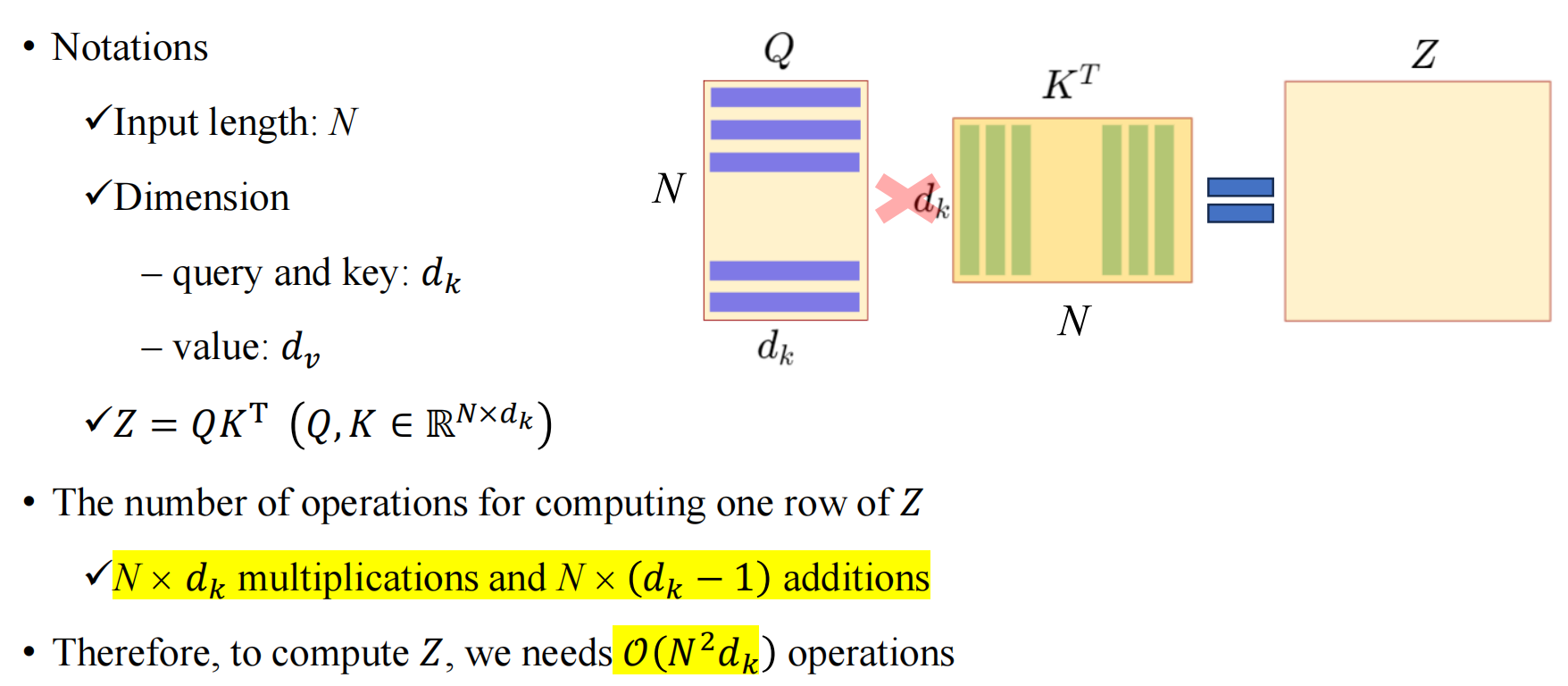
(1)时间复杂度
(2)空间复杂度
参考资料
- 深度学习500问
- 邱锡鹏,神经网络与深度学习,机械工业出版社,https://nndl.github.io/, 2020.